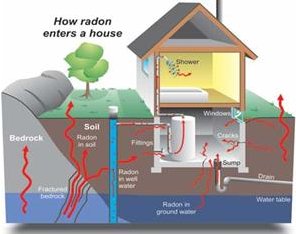
Like all of the radioactive elements radon has a half life. It decays at a steady rate so that after a certain time any given quantity of radon will be reduced by half the original amount. Compared to Uranium 238 which has a half life of 4.5 billion years and radium which has a half life of 1630 years, radon has a very short half life of a mere 3.7 days. In addition to its extremely short life span radon also differs from its parental elements in one other very important way. While uranium and radium are metals trapped in the soil,Radon is a gas and because of this metamorphic change it behaves very differently. Radon escapes from the soil.
From the instant of its formation the gas begins to move towards the surface. It follows the path of least resistance in much the same way that water tends to flow towards its lowest level in accordance with the demands of gravity. Radon moves upwards through the soil in accordance with the negative pressure zones within the soil.
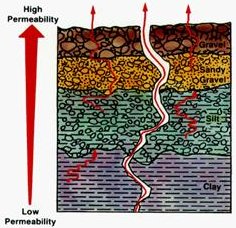
Negative pressure is best thought of as empty space. It can also be visualized as a vacuum because there is always a pressure differential that exists between empty space and occupied space. From our perspective it would seem that there would be very little empty space available in the soil. From the perspective of an atom, however, this is not true. In the microcosm as well as the macrocosm the void is everywhere.